Вот мы все и добрались до первого листка с настоящими заданиями. Как их выполнять, что делать? В первой части вы найдёте список задач, которые предлагается выполнить. Очень рекомендуем хотя бы попытаться решить их самостоятельно, попробовать разные подходы, обсудить с друзьями или взять тетрадку с собой во время прогулки в парк. Самые нетерпеливые (а также те, кто достиг успехов в решении), могут прокрутить страницу ниже, где обнаружат максимально подробное решение каждой из задач. Надеемся, они вам помогут. Если что не ясно — спрашивайте в комментариях. Удачи!
Задача 1
Записать элементы множества ![]() , если
, если ![]() , и
, и ![]() .
.
Задача 2
Теперь давайте докажем три более абстрактных тезиса: 1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() .
.
Задача 3
В гимназии учатся ![]() учеников, нам известно, что каждый из них знает греческий или латынь, а некоторые даже оба. Известно, что
учеников, нам известно, что каждый из них знает греческий или латынь, а некоторые даже оба. Известно, что ![]() из них знают греческий язык (множество
из них знают греческий язык (множество ![]() ) и
) и ![]() знают латынь (множество
знают латынь (множество ![]() ). Какая часть учащихся знает оба языка?
). Какая часть учащихся знает оба языка?
Задача 4
Ещё раз вспомните из лекции, что такое мощность множества. А теперь давайте попробуем доказать справедливость равенства ![]() .
.
Задача 5
Пол комнаты площадью в шесть квадратных метров полностью покрыт тремя коврами, площадь каждого из которых равна три квадратных метра. Докажите, что какие-то два из этих ковров перекрываются по площади, не меньшей одного квадратного метра.
Задача 6
Лесник считал сосны в лесу. Он обошёл территории, условно обозначенными кругами на рисунке ниже, и внутри каждого круга насчитал ровно пять сосен. Мог ли получиться у лесника на самом деле такой результат, или он ошибся?

Задача 7
Пусть от нас требуется показать истинность утверждения ![]() , давайте сделаем это!
, давайте сделаем это!
Задача 8
Если ![]() , то докажем, что
, то докажем, что ![]() .
.
SPOILER ALERT! ДАЛЬШЕ ИДУТ РЕШЕНИЯ, НАСТОЯТЕЛЬНО РЕКОМЕНДУЕМ СНАЧАЛА ПОПРОБОВАТЬ!
Задача 1
Записать элементы множества ![]() , если
, если ![]() , и
, и ![]() .
.
Решение:
Рассмотрим первый случай — мы имеем дело с объединением множеств, и в объединении, например, множеств ![]() , как мы помним из лекции, собираются вместе все элементы из множеств
, как мы помним из лекции, собираются вместе все элементы из множеств ![]() и
и ![]() . Заметим, что множества имеют общие элементы — а именно,
. Заметим, что множества имеют общие элементы — а именно, ![]() и
и ![]() . Поэтому мы не должны случайно упомянуть их повторно, пока собираем «в кучу» оба наших множества.
. Поэтому мы не должны случайно упомянуть их повторно, пока собираем «в кучу» оба наших множества.
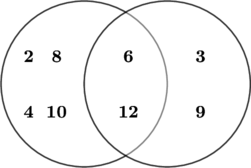
В итоге получим ![]()
По второму пункту мы, фактически, ответ уже нашли —ведь в пересечение множеств входят общие элементы этих множеств, а мы их уже установили — это ![]() и
и ![]() . Поэтому
. Поэтому ![]()
В третьем случае от нас требуется узнать разность множеств: ![]() . Из лекции мы помним, что в множество
. Из лекции мы помним, что в множество ![]() должны войти все элементы, которые входят в
должны войти все элементы, которые входят в ![]() и только в
и только в ![]() . Все элементы, которые входят в
. Все элементы, которые входят в ![]() , мы должны отбросить. Значит, мы должны отбросить
, мы должны отбросить. Значит, мы должны отбросить ![]() , которые присутствуют в
, которые присутствуют в ![]() и не присутствуют в
и не присутствуют в ![]() , а также отбросить
, а также отбросить ![]() и
и ![]() , которые располагаются одновременно в двух этих множествах.
, которые располагаются одновременно в двух этих множествах.
В итоге получаем, что ![]() .
.
А что же от нас требуют в последнем случае? ![]() — таким образом обозначается разность универсального множества
— таким образом обозначается разность универсального множества ![]() с множеством, расположенным под чертой (дополнение множества
с множеством, расположенным под чертой (дополнение множества ![]() в
в ![]() ).
).
Введём понятие универсального множества ![]() — это совокупность всех элементов, которые фигурируют в нашем задаче/рассмотрении в целом. Все элементы, которые «есть» в этом конкретном контексте. Допустим, если мы анализируем холодильники разных марок и сортируем их по признакам (а значит и распределяем по разным множествам), то логично брать в данном случае в качестве универсального множества всю совокупность существующих и когда-либо существовавших холодильников. Как легко видеть, мы сами вольны устанавливать границы универсального множества
— это совокупность всех элементов, которые фигурируют в нашем задаче/рассмотрении в целом. Все элементы, которые «есть» в этом конкретном контексте. Допустим, если мы анализируем холодильники разных марок и сортируем их по признакам (а значит и распределяем по разным множествам), то логично брать в данном случае в качестве универсального множества всю совокупность существующих и когда-либо существовавших холодильников. Как легко видеть, мы сами вольны устанавливать границы универсального множества ![]() . Однако оно всегда должно быть таким, чтобы в рамках нашей задачи нам не попалось ни одного элемента, который мог бы оказаться вне
. Однако оно всегда должно быть таким, чтобы в рамках нашей задачи нам не попалось ни одного элемента, который мог бы оказаться вне ![]() ! В этом и состоит смысл и удобство универсального множества.
! В этом и состоит смысл и удобство универсального множества.
Мы предположим, что универсальное множество в данном случае состоит из всех элементов, которые указаны в условии задачи — нетрудно видеть, что в таком случае универсальное множество ![]() будет тождественно
будет тождественно ![]() .
.
Значит, осталось лишь найти разность ![]() . Это будут все элементы универсального множества за вычетом тех, которые входят в
. Это будут все элементы универсального множества за вычетом тех, которые входят в ![]() . Из предыдущего случая мы знаем, что
. Из предыдущего случая мы знаем, что ![]() .
.
Значит, ![]()
Задача 2
Теперь давайте докажем три более абстрактных тезиса: 1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() .
.
Решение:
Случай первый. Опираясь на выводы предыдущей задачи, мы понимаем, что ![]() указывает на разность универсального множества с множеством, расположенным под чертой (в данном случае некое
указывает на разность универсального множества с множеством, расположенным под чертой (в данном случае некое ![]() ).
).
На картинке прямоугольник представляет собой универсальное множество ![]() , а круг — множество
, а круг — множество ![]() . Разность
. Разность ![]() — это пространство между квадратом и кругом. Запомним, что светло-розовым цветом у нас отмечается «исходное» множество, относительно которого берётся дополнение, а серым — само дополнение к этому «исходному» множеству.
— это пространство между квадратом и кругом. Запомним, что светло-розовым цветом у нас отмечается «исходное» множество, относительно которого берётся дополнение, а серым — само дополнение к этому «исходному» множеству.
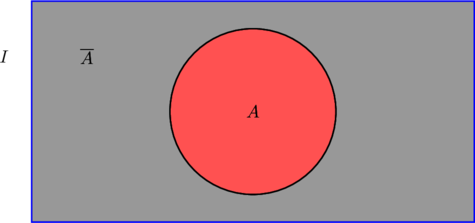
Теперь разность между прямоугольником и кругом должна стать «исходным» множеством. Где же будет его дополнение? Правильно, в круге!
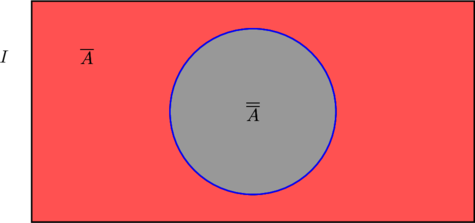
Более формально это можно установить следующим образом. По определению, если ![]() , то
, то ![]() . Иными словами, все элементы, которые входят в
. Иными словами, все элементы, которые входят в ![]() , не входят в дополнение к
, не входят в дополнение к ![]() по определению (поскольку имеет место разность множеств, а разность «выкидывает» из рассмотрения все элементы «вычитаемого» множества).
по определению (поскольку имеет место разность множеств, а разность «выкидывает» из рассмотрения все элементы «вычитаемого» множества).
Но в таком случае что мешает нам распространить ту же логику на дополнение дополнения? Если ![]() , то
, то ![]() . И наоборот: если
. И наоборот: если ![]() , то
, то ![]() .
.
Совмещаем оба полученных результата: с одной стороны, если ![]() , то
, то ![]() . Но для всех
. Но для всех ![]() выполняется, что
выполняется, что ![]() . Что и требовалось доказать.
. Что и требовалось доказать.
Случай второй. По определению универсального множества, абсолютно все элементы в нашем рассмотрении принадлежат множеству ![]() . А значит, элементов, которые бы не входили в множество
. А значит, элементов, которые бы не входили в множество ![]() , в рамках нашей задачи просто не существует. Иными словами, дополнение к универсальному множеству — пустое множество.
, в рамках нашей задачи просто не существует. Иными словами, дополнение к универсальному множеству — пустое множество.
Случай третий. По аналогии: если к множеству не относится ни один из элементов, рассматриваемых нами, то это пустое множество. Но это значит, что абсолютно все элементы, о которых мы можем помыслить в рамках нашей задачи, относятся к дополнению этого множества (дополнению пустого множества). Значит, дополнение пустого множества совпадает с универсальным множеством.
Задача 3
В гимназии учатся ![]() учеников, нам известно, что каждый из них знает греческий или латынь, а некоторые даже оба. Известно, что
учеников, нам известно, что каждый из них знает греческий или латынь, а некоторые даже оба. Известно, что ![]() из них знают греческий язык (множество
из них знают греческий язык (множество ![]() ) и
) и ![]() знают латынь (множество
знают латынь (множество ![]() ). Какая часть учащихся знает оба языка?
). Какая часть учащихся знает оба языка?
Решение:
Число всех учеников в данном случае можно представить как универсальное множество ![]() . Изобразим его в качестве прямоугольника. В условии сказано, что знатоки греческого и/или латыни исчерпывают всю совокупность учащихся без остатка, а потому данные подмножества вместе должны образовать исходный прямоугольник как на картинке. В данном случае мы частично «наложили» друг на друга два подмножества, чтобы у них образовалось пересечение.
. Изобразим его в качестве прямоугольника. В условии сказано, что знатоки греческого и/или латыни исчерпывают всю совокупность учащихся без остатка, а потому данные подмножества вместе должны образовать исходный прямоугольник как на картинке. В данном случае мы частично «наложили» друг на друга два подмножества, чтобы у них образовалось пересечение.

Итак, нам известно, что все из 200 учеников знают по крайней мере либо греческий язык, либо латынь. Однако если мы предположим, что эти множества не пересекаются, и сложим число знатоков греческого с числом знатоков латыни, мы получим ![]() человек. Это значение превышает численность учеников гимназии. Значит, некоторые люди действительно знают оба языка.
человек. Это значение превышает численность учеников гимназии. Значит, некоторые люди действительно знают оба языка.
Как же выяснить, сколько людей входят в это пересечение двух множеств? Мы знаешь лишь один критерий, по которому можно это установить — пойти от обратного, для начала выявив число знатоков только одного языка. Ведь те, кто знают только один язык, в пересечение точно не войдут!
Кто же не знает греческий? ![]() . Пусть это множество
. Пусть это множество ![]() . А латынь не знают
. А латынь не знают ![]() человек. Пусть это будет множество
человек. Пусть это будет множество ![]() . Теперь нам осталось заметить, что людей, которые бы знали только один язык, вне объединения этих двух множеств не существует! Действительно, если бы такой человек, знающий только один язык, существовал, не попадая в множество
. Теперь нам осталось заметить, что людей, которые бы знали только один язык, вне объединения этих двух множеств не существует! Действительно, если бы такой человек, знающий только один язык, существовал, не попадая в множество ![]() , то получалось бы, что мы не досчитались либо не знающего греческий, либо не знающего латынь в множествах
, то получалось бы, что мы не досчитались либо не знающего греческий, либо не знающего латынь в множествах ![]() или
или ![]() соответственно. А это не так — мы посчитали абсолютно всех.
соответственно. А это не так — мы посчитали абсолютно всех.
Выходит, что ![]() (здесь мы обращаемся к понятию мощности множества, которое было определено в лекции) составляет число тех, кто знает только один язык. Отсюда, наконец, следует, что
(здесь мы обращаемся к понятию мощности множества, которое было определено в лекции) составляет число тех, кто знает только один язык. Отсюда, наконец, следует, что ![]() человек говорят на обоих языках.
человек говорят на обоих языках.
Задача 4
Ещё раз вспомните из лекции, что такое мощность множества! А теперь давайте попробуем доказать справедливость равенства
![]() .
.
Решение:
Ух, сложно! Но давайте начнём разбираться последовательно. Эта формула имеет вид для трёх произвольных множеств. Но вовсе не обязательно сразу рваться в бой — можно приступить к задаче с рассмотрения самого простого случая, а затем «насытить» наш анализ дополнительными моментами. Случай с одним множеством, правда, рассматривать бессмысленно — уж слишком он тривиален. Поэтому предлагаем подумать, как посчитать число элементов множеств, если их всего два.
Допустим, что эти множества не пересекаются. Тогда сумма числа их элементов находится легко — просто складываем в одну кучу все подряд элементы из обеих множеств.
Но что будет, если пересечение всё-таки имеет место быть? Из первой задачи мы видели, что в таком случае, если просто сложить все элементы из первого и второго множества, неизбежна ситуация повторного счёта. Для того, чтобы этого избежать, в задаче 1 нам пришлось обратить внимание на объединение множеств и сойтись на том, что элементы этого подмножества должны считаться лишь единожды, а не дважды.
В общем случае действует та же самая логика. Какие-то элементы у нас неизбежно засчитаются дважды — это будут те из них, которые содержатся одновременно и в ![]() , и в
, и в ![]() . И чтобы удалить лишнюю «накрутку» достаточно просто вычесть число элементов, составляющих пересечение
. И чтобы удалить лишнюю «накрутку» достаточно просто вычесть число элементов, составляющих пересечение ![]() (таким образом от двойного счёта мы вернёмся вновь к одинарному). Итак, сначала, «в тупую» складывая все элементы обоих множеств, мы лишний раз какие-то из них прибавляем (, конечно, не «какие-то», а входящие в пересечение
(таким образом от двойного счёта мы вернёмся вновь к одинарному). Итак, сначала, «в тупую» складывая все элементы обоих множеств, мы лишний раз какие-то из них прибавляем (, конечно, не «какие-то», а входящие в пересечение ![]() ), а затем вновь их вычитаем. Один раз.
), а затем вновь их вычитаем. Один раз.
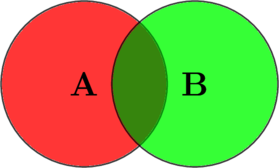
Обобщим данное правило вычисления в формуле ![]() . Обратите внимание, что этому правилу подчиняется и первый из наших случаев (где не было пересечения) — просто в этом варианте последнее слагаемое формулы будет равно нулю.
. Обратите внимание, что этому правилу подчиняется и первый из наших случаев (где не было пересечения) — просто в этом варианте последнее слагаемое формулы будет равно нулю.
Ну а теперь можно перейти к трём множествам. Как вы, наверное, уже догадались, в этом случае можно предположить гораздо более разнообразные случаи пересечения множеств ![]() ,
, ![]() , и
, и ![]() .
.
В частности, возможны сочетания ![]() ,
, ![]() ,
, ![]() — всего три штуки. Кроме того, добавляется ещё случай
— всего три штуки. Кроме того, добавляется ещё случай ![]() .
.
Какие именно из этих пересечений пустые, а какие нет, мы знать заведомо не можем. Однако если какие-то из них не пустые, то мы должны их грамотно вычитать (или прибавлять), чтобы по-прежнему избегать возможности повторного (а то и тройного) счёта.
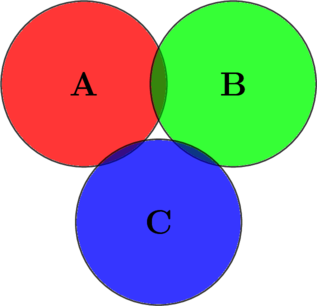
Как и в предыдущем случае, мы должны вычитать пересечения двух множеств — даже если этого пересечения нет, от вычитания нуля нам хуже не станет. По умолчанию будем исходить из того, что в результате сложения ![]() у нас неизбежно возникают повторяющиеся элементы. Предположим, что повторения встречаются только в пересечениях не более двух множеств (например,
у нас неизбежно возникают повторяющиеся элементы. Предположим, что повторения встречаются только в пересечениях не более двух множеств (например, ![]() ). Тогда, в соответствии с прошлым примером, мы должны просто вычесть число элементов в этих пересечениях:
). Тогда, в соответствии с прошлым примером, мы должны просто вычесть число элементов в этих пересечениях: ![]() .
.
Изобразим этот случай — когда есть попарные пересечения, но нет пересечения тройного:
Однако у нас есть ещё один вариант пересечения — сразу всех трёх множеств вместе! В случае наличия трёх множеств ![]() такой вариант единственный. Это
такой вариант единственный. Это ![]() . И если вы в этом не уверены, то задумайтесь — какие ещё варианты мы можем помыслить? Разве что
. И если вы в этом не уверены, то задумайтесь — какие ещё варианты мы можем помыслить? Разве что ![]() или
или ![]() … Но это будут повторения одного и того же множества! Так что в этом случае тройное пересечение только одно — как и в случае двух множеств единственным было пересечение двух множеств.
… Но это будут повторения одного и того же множества! Так что в этом случае тройное пересечение только одно — как и в случае двух множеств единственным было пересечение двух множеств.
Хорошо, скажете вы, но что же делать с этим пересечением этих трёх множеств? Прибавлять число элементов, входящих в это множество, или отнимать?
Для того, чтобы ответить на этот вопрос, необходимо хорошенько подумать, сколько раз у нас «считались» и вычитались элементы, входящие в это самое ![]() . Сначала они засчитались при подсчёте элементов
. Сначала они засчитались при подсчёте элементов ![]() , затем
, затем ![]() , затем
, затем ![]() — троекратно! Ведь элемент, входящий в пересечение сразу трёх множеств, входит в каждое из этих трёх множеств по определению… А потом эти же элементы были удалены также три раза — из-за вычитания элементов трёх множеств
— троекратно! Ведь элемент, входящий в пересечение сразу трёх множеств, входит в каждое из этих трёх множеств по определению… А потом эти же элементы были удалены также три раза — из-за вычитания элементов трёх множеств ![]() . Значит, в итоге осталось ноль элементов! Поэтому получается, что число элементов этого пересечения нужно прибавить и итоговая формула примет вид
. Значит, в итоге осталось ноль элементов! Поэтому получается, что число элементов этого пересечения нужно прибавить и итоговая формула примет вид ![]() .
.
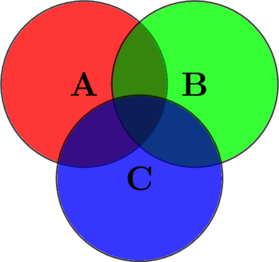
Обратите внимание, что количество слагаемых точно соответствует числу пересечений и разностей множеств на изображении выше.
PS. Этот случай можно распространить и на большее число множеств, но тогда нам нужно будет пересчитывать все комбинации из двух, трёх… и ![]() множеств. Как именно можно «обобщить» такое перечисление, нас пока не интересует — это слишком далеко выходит за нашу тему. Однажды мы к этому вопросу вернёмся. Но внимательный читатель может обратить внимание, что каждый раз по мере увеличения числа множеств, «участвующих» в пересечении, знак будет меняться с минуса на плюс и с плюса на минус.
множеств. Как именно можно «обобщить» такое перечисление, нас пока не интересует — это слишком далеко выходит за нашу тему. Однажды мы к этому вопросу вернёмся. Но внимательный читатель может обратить внимание, что каждый раз по мере увеличения числа множеств, «участвующих» в пересечении, знак будет меняться с минуса на плюс и с плюса на минус.
Подумайте: если у нас было бы не три, а четыре множества, то получилось бы, что при учёте четырёхкратного пересечения ![]() у нас будет вновь повторный счёт из-за того, что элементы множеств
у нас будет вновь повторный счёт из-за того, что элементы множеств ![]() будут засчитаны с положительным знаком. Значит,
будут засчитаны с положительным знаком. Значит, ![]() будет вычитаться из общей суммы элементов.
будет вычитаться из общей суммы элементов.
Отсюда общая формула:
![]()
Задача 5
Пол комнаты площадью в шесть квадратных метров полностью покрыт тремя коврами, площадь каждого из которых равна три квадратных метра. Докажите, что какие-то два из этих ковров перекрываются по площади, не меньшей одного квадратного метра.
Решение:
Один из часто используемых методов в математических доказательствах — движение от обратного. Мы его уже однажды применили. Попробуем применить его и здесь. Допустим для начала, что площадь покрывается коврами вполне возможна без перекрытия вообще (без пересечения).
Мы знаем, что площадь каждого из трёх ковров составляет ![]() квадратных метра. Мы имеем полное право представить наши ковры в качестве множеств. Если они лежат без перекрытия, то их общая площадь является просто суммой их отдельных площадей:
квадратных метра. Мы имеем полное право представить наши ковры в качестве множеств. Если они лежат без перекрытия, то их общая площадь является просто суммой их отдельных площадей: ![]() , что больше площади комнаты в
, что больше площади комнаты в ![]() квадратных метров. Мы пришли к противоречию, предположив обратное. Значит, ковры должны перекрываться.
квадратных метров. Мы пришли к противоречию, предположив обратное. Значит, ковры должны перекрываться.
Тогда давайте предположим, что площадь каждого из попарных перекрытий ковров (первый с третьим, второй с третьим, второй с первым) может составлять меньше одного квадратного метра. И снова мы вводим предположение, обратное тому, которое мы хотим доказать.
Действительно, обратите внимание: чтобы опровергнуть тезис «какие-то два из этих ковров обязательно перекрываются по площади, не меньшей одного квадратного метра», нам нужно продемонстрировать, что абсолютно все перекрытия неизбежно имеют площадь, меньшую чем один квадратный метр. Обзовём последнее нашим условием-гипотезой.
Допустим, что какие-то два ковра перекрываются таким образом, чтобы удовлетворять данному условию. Есть ковёр ![]() и ковёр
и ковёр ![]() , и их площадь перекрытия
, и их площадь перекрытия ![]() кв. м.
кв. м.
В таком случае их общая площадь обязательно должна превышать 5 кв. м, но не быть более 6 кв. м (потому что оба ковра не крупнее трёх квадратных метров каждый). Таким образом, их общая площадь равна ![]() кв. м.
кв. м.
Теперь перейдём к третьему ковру. Опять же по нашему предположению от обратного, он должен иметь общую площадь с первым ковром меньшую, чем квадратный метр (обозначим её как ![]() ), и со вторым ковром (
), и со вторым ковром (![]() ) — также меньшую, чем квадратный метр. Рассмотрим максимальный случай —
) — также меньшую, чем квадратный метр. Рассмотрим максимальный случай — ![]() и
и ![]() займут максимальную площадь вместе в том случае, если они друг с другом не пересекаются. Тогда общая площадь объединения
займут максимальную площадь вместе в том случае, если они друг с другом не пересекаются. Тогда общая площадь объединения ![]() будет «почти» достигать
будет «почти» достигать ![]() квадратных метра. Следовательно, оставшаяся часть третьего ковра (назовём её
квадратных метра. Следовательно, оставшаяся часть третьего ковра (назовём её ![]() ) должна покрывать площадь большую, чем
) должна покрывать площадь большую, чем ![]() квадратный метр, поскольку из площади третьего ковра в 3 кв. м. вычитается площадь «общего» покрытия, составляющую менее двух метров: например,
квадратный метр, поскольку из площади третьего ковра в 3 кв. м. вычитается площадь «общего» покрытия, составляющую менее двух метров: например, ![]() .
.
Однако площадь, покрытая первыми двумя коврами, составляет ![]() кв. м. Третий же ковёр добавляет площадь, большую, чем квадратный метр. А значит
кв. м. Третий же ковёр добавляет площадь, большую, чем квадратный метр. А значит ![]() , то есть все три ковра занимают площадь большую, чем площадь квартиры, при выполнении нашего условия-гипотезы. Мы пришли к противоречию.
, то есть все три ковра занимают площадь большую, чем площадь квартиры, при выполнении нашего условия-гипотезы. Мы пришли к противоречию.
Задача 6
Лесник считал сосны в лесу. Он обошёл территории, условно обозначенными кругами на рисунке ниже, и внутри каждого круга насчитал ровно пять сосен. Мог ли получиться у лесника на самом деле такой результат, или он ошибся?

Решение:
Опять же можно пойти уже исследованным нам ходом рассуждения — движением от противного. Если в каждом круге действительно по пять сосен, то, если собрать вместе все маленькие круги, таких деревьев должно быть как минимум 15. Однако большие круги свидетельствуют о не более чем 10 соснах, что входит в противоречие с предыдущим утверждением.
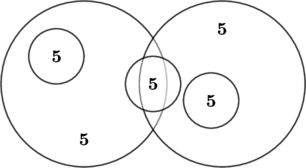
Альтернативно можно обнаружить противоречие, наблюдая за расположением деревьев в пересечениях множеств. Малые левый и правый круги располагаются таким образом, что других сосен в больших кругах быть не должно. Но если это так, то на центральный малый круг не хватит вообще ни одной сосны, что опять же противоречит условию. Это хорошо видно на рисунке выше.
Задача 7
Пусть от нас требуется показать истинность утверждения:
![]()
Решение:
Внимательно рассмотрим, для каких элементов у нас будет выполняться выражение в левой части тождества. Опять же, первым делом нам необходимо вспомнить определения. ![]() вмещает в себя все элементы
вмещает в себя все элементы ![]() такие, что для них выполняется
такие, что для них выполняется ![]() и
и ![]() одновременно. Таким образом, в эту разность входят те элементы
одновременно. Таким образом, в эту разность входят те элементы ![]() , которые не содержатся в
, которые не содержатся в ![]() . Таким образом отсюда исключаются как элементы, не содержащиеся в
. Таким образом отсюда исключаются как элементы, не содержащиеся в ![]() вообще, так и содержащиеся в
вообще, так и содержащиеся в ![]() , но одновременно и входящие в
, но одновременно и входящие в ![]() — то есть располагающиеся в пересечении
— то есть располагающиеся в пересечении ![]() .
.
В данном случае розовым цветом обозначено множество, «остающееся» после разности.
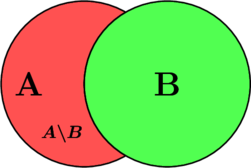
Аналогично рассуждение для ![]() . В этом множестве теперь будут находиться все элементы, которые входят в
. В этом множестве теперь будут находиться все элементы, которые входят в ![]() , не находясь в то же время в
, не находясь в то же время в ![]() .
.
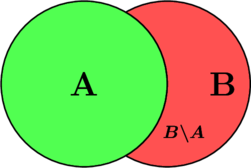
Выходит, из обеих вышеуказанных множеств исключается одно и то же пересечение ![]() .
.
Однако третья скобка в исходном выражении как раз и возвращает нам утерянное: ![]() . Тем самым, в итоге в состав нашего множества входят все элементы, входящие только в
. Тем самым, в итоге в состав нашего множества входят все элементы, входящие только в ![]() , только в
, только в ![]() , а также одновременно в
, а также одновременно в ![]() и
и ![]() . Что это за множество у нас тогда получилось? Верно,
. Что это за множество у нас тогда получилось? Верно, ![]() !
!
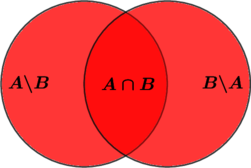
Задача 8
Если ![]() , то
, то ![]() .
.
Решение:
Ранее мы видели, что в сложных утверждениях на языке теории множеств одновременно может предполагаться огромное количество различных ситуаций: какие-то множества пересекаются друг с другом, какие-то лежат внутри друг друга или, наоборот, располагаются порознь. Каждая из таких ситуаций образует частный случай записанного утверждения, и порой перебрать все из них тяжело. Как же доказывать такие утверждения, не тратя слишком много времени и сил? Рассуждая по существу с помощью формальной записи всех условий. Мы это проделывали уже раньше, но теперь сделаем это в более явном виде.
В данном случае нам нужно фактически показать, что при предпосылке ![]() всякий
всякий ![]() также принадлежит и
также принадлежит и ![]() .
.
Расшифруем первое выражение ![]() . Оно означает выполнение одновременно двух условий:
. Оно означает выполнение одновременно двух условий: ![]() и
и ![]() .
.
Теперь обратим внимание на то, выполняется ли при этой предпосылке ![]() для нашего
для нашего ![]() . Вспомним опять про нашего предположение из условия задачи, что
. Вспомним опять про нашего предположение из условия задачи, что ![]() . В таком случае, по определению подмножества, следует, что если
. В таком случае, по определению подмножества, следует, что если ![]() , автоматически выполняется и
, автоматически выполняется и ![]() . С другой стороны, если
. С другой стороны, если ![]() , то и
, то и ![]() — в противном случае элемент
— в противном случае элемент ![]() содержался бы в
содержался бы в ![]() , но не содержался бы в
, но не содержался бы в ![]() и мы пришли бы к противоречию.
и мы пришли бы к противоречию.
Соответственно, с учётом условия ![]() приходим к тому, что выполнение
приходим к тому, что выполнение ![]() вместе с
вместе с ![]() приводит к выполнению
приводит к выполнению ![]() и
и ![]() , что и требовалось показать.
, что и требовалось показать.
Задача 9
Доказать справедливость выражения ![]()
Решение:
Для начала вспомним, что означает разность множеств. В данном это значит, что некий элемент ![]() должен одновременно удовлетворять двум условиям: принадлежать
должен одновременно удовлетворять двум условиям: принадлежать ![]() и при этом не принадлежать
и при этом не принадлежать ![]() .
.
Теперь давайте хорошенько осознаем, что именно за выражение сформулировано в нашем задании. Нам необходимо установить, что в случае, если элемент входит в множество ![]() , то он входит и в множество, представленное в виде
, то он входит и в множество, представленное в виде ![]() . Это обстоятельство и отражается тем фактом, что второе множество представлено подмножеством первого. Иными словами, если элемент входит во второе множество, то автоматически входит и в первое — аналогичный случай мы рассматривали и в предыдущей задаче 7.
. Это обстоятельство и отражается тем фактом, что второе множество представлено подмножеством первого. Иными словами, если элемент входит во второе множество, то автоматически входит и в первое — аналогичный случай мы рассматривали и в предыдущей задаче 7.
В этом заключается смысл выражения, истинность которого нам необходимо установить.
Итак, мы исходим из того, что какой-то элемент ![]() входит в множество
входит в множество ![]() .
.
В нашей задаче фигурирует также множество ![]() . В отношении этого множества наш элемент
. В отношении этого множества наш элемент ![]() может находиться в двух состояниях: либо он входит в состав
может находиться в двух состояниях: либо он входит в состав ![]() , либо нет. Рассмотрим для начала второй вариант.
, либо нет. Рассмотрим для начала второй вариант.
Если ![]() , но в то же время верно, что
, но в то же время верно, что ![]() (не забываем, что последнее мы принимаем в качестве предпосылки в наших рассуждениях!), то выполнится и условие
(не забываем, что последнее мы принимаем в качестве предпосылки в наших рассуждениях!), то выполнится и условие ![]() , а вместе с ним и
, а вместе с ним и ![]() .
.
Теперь рассмотрим другой случай: пусть ![]() .
.
Опять обратимся к нашей предпосылке, которая гласит, что ![]() . Это означает, что элемент
. Это означает, что элемент ![]() в данном случае входит в состав
в данном случае входит в состав ![]() , но не входит в состав
, но не входит в состав ![]() (согласно предпосылке). Соединяя эти две идеи в одну мы можем сказать, что элемент
(согласно предпосылке). Соединяя эти две идеи в одну мы можем сказать, что элемент ![]() . Таким образом, в этом выполняется выражение
. Таким образом, в этом выполняется выражение ![]() .
.
Таким образом, мы исчерпали все возможные состояния, которые может принимать ![]() и пришли к выводу, что всегда будет выполняться одно из двух условий: либо
и пришли к выводу, что всегда будет выполняться одно из двух условий: либо ![]() , либо
, либо ![]() .
.
А почему из выполнения хотя бы одного из двух этих условий следует и выполнение ![]() ?
?
Потому что мы в данном случае имеем объединение — а оно у нас «имеет силу» тогда, когда выполняется хотя бы что-то одно: либо истинно выражение слева от нашей подковы (в данном случае ![]() ), либо справа (в данном случае
), либо справа (в данном случае ![]() ), либо оба.
), либо оба.
Опять же, в нашем случае невозможно, чтобы оба условия не выполнялись одновременно, ибо каждому из них соответствует один из двух случаев: либо ![]() , либо
, либо ![]() , что исчерпывает все возможные варианты в принципе. Значит, при предпосылке
, что исчерпывает все возможные варианты в принципе. Значит, при предпосылке ![]() объединение
объединение ![]() всегда будет гарантированно выполняться.
всегда будет гарантированно выполняться.
Comments ( 32 )