Как не потерять то, что вам действительно дорого? В самом буквальном смысле, то есть мы тут не об исчезнувших родственниках, подростковых влюблённостях и у же тем более не о радостях отцовства говорим. Куда чаще проблемы с потерями возникают в случае ключей от квартиры, телевизионного пульта или джойстика PS4, как всё это случайно вместе с мусором не выкинуть? Ответ ясен и знаком любому, кто с этим сталкивался — следует надёжно привязать.
Говорят, что есть ещё один метод — «класть всё на своё место», но за очевидной фантастичностью мы его сразу вычёркиваем. Будем привязывать, да покрепче. Привязка вообще хороша именно тем, что не обязательно должна быть особо короткой, даже наоборот, ничто не мешает растянуть клубок на несколько десятков метров. Главное в ней это надёжность, крепкий материал, благодаря которому всегда можно от одного места (где начало привязи, допустим, в районе торшера) дойти до другого (где и находится PS4 контролер, а то GTA V сама в себя не поиграет).
Всё сказанное не вызывает у вас внутреннего протеста и бури непонимания? Нет? Значит, вы вполне разбираетесь в том, что такое функциональная связь и готовы с этим плодотворным понятием всячески работать. Только вместо ключей и пульта придётся иметь дело с разнообразными и достаточно абстрактными математическими элементами.

Функция — это когда связь есть. Крепкая-крепкая. Как дружба. Как если брат к тебе хорошо относится. Как тренер по борьбе, к которому ты в детстве ходишь. Понятно объясняю, да?
Делу отнюдь не помогает то, что, по традиции, записываются все эти элементы и связи совершенно чудовищным, неинтуитивным образом. Это приводит к тому, что многие ученики, имеющие несчастье с подобными идеями постоянно сталкиваться, считают, что единственный выход — просто наизусть выучить правила записи, не понимая, что они в принципе должны обозначать.
И правда ведь, почему ![]() называется «функцией от
называется «функцией от ![]() «, зачем тут стоят скобки, почему одно располагается рядом с другим? Разве мы что-то умножаем? Да и вообще, как это всё понять на примере кружочков, квадратиков и стрелочек?
«, зачем тут стоят скобки, почему одно располагается рядом с другим? Разве мы что-то умножаем? Да и вообще, как это всё понять на примере кружочков, квадратиков и стрелочек?
Понять это крайне просто. И да, кружочки тут окажутся хорошим подспорьем, как и вообще те минимальные знания по теории множеств, которые в самом начале казались избыточными (не зря же мы просили нам довериться!).
Не считая примеров с ключами и пультами управления, наиболее простым способом представить себе смысл понятия функции является концепция «отображения», с изучения которой только и могут начинаться все дальнейшие упражнения такого плана. Начнём пояснение с одного-единственного множества, обозначаемого как ![]() .
.

Как и любое порядочное множество, ![]() состоит из элементов типа
состоит из элементов типа ![]() и прочих. Нам совершенно не важно, сколько таких
и прочих. Нам совершенно не важно, сколько таких ![]() в принципе — главное, что больше нуля, т.е. что множество
в принципе — главное, что больше нуля, т.е. что множество ![]() не является пустым. Мы хотим эти элементы с чем-нибудь связать, формируя прочную, сильнее всех возможных обстоятельств и случайных измен, взаимосвязь. Добиться этого можно, конкретно указав, что и с чем связывается, да так, чтобы это нельзя было случайно перепутать.
не является пустым. Мы хотим эти элементы с чем-нибудь связать, формируя прочную, сильнее всех возможных обстоятельств и случайных измен, взаимосвязь. Добиться этого можно, конкретно указав, что и с чем связывается, да так, чтобы это нельзя было случайно перепутать.
Допустим, возьмём уже знакомое множество натуральных чисел ![]() и свяжем его элементы с точками на прямой, получив тем самым числовую ось (для простоты ограничимся тремя числами):
и свяжем его элементы с точками на прямой, получив тем самым числовую ось (для простоты ограничимся тремя числами):
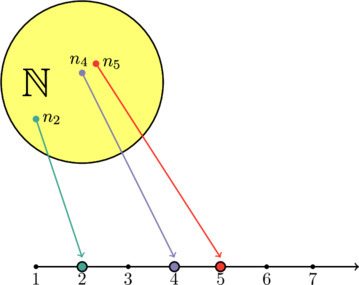
Хотя мы не проделали ровным счётом ничего существенного, но теперь мы можем удобно представлять смысл операций в ![]() на примере простых движений влево и вправо. Собственно, используя этот факт, мы и ознакомились с основами арифметики. Где гарантия того, что наши шаги по числовой прямой не приведут к чему-то, что не следует из исходного множества? А она в том, что мы установили все связи совершенно однозначно, хотя при увеличении числа элементов в самих стрелочках можно и запутаться. Да и вообще иногда оказывается, что если привязать одно к другому, с этим другим работать куда проще.
на примере простых движений влево и вправо. Собственно, используя этот факт, мы и ознакомились с основами арифметики. Где гарантия того, что наши шаги по числовой прямой не приведут к чему-то, что не следует из исходного множества? А она в том, что мы установили все связи совершенно однозначно, хотя при увеличении числа элементов в самих стрелочках можно и запутаться. Да и вообще иногда оказывается, что если привязать одно к другому, с этим другим работать куда проще.
Теперь давайте чуть понизим градус визуальности изложения и будем говорить только о множествах. Потребовалось связать между собой ![]() и какое-то другое множество под именем
и какое-то другое множество под именем ![]() . Если элементов не так много, то и проблем не так много, просто всех инструктируем, что
. Если элементов не так много, то и проблем не так много, просто всех инструктируем, что ![]() у нас теперь связано с
у нас теперь связано с ![]() ,
, ![]() с
с ![]() и так далее. Нечто схожее делает ваша соседка по лестничной клетке во время душевных бесед с жильцами дома, пытаясь создать стойкую связь между «гости вашей квартиры» и «конченые наркоманы»:
и так далее. Нечто схожее делает ваша соседка по лестничной клетке во время душевных бесед с жильцами дома, пытаясь создать стойкую связь между «гости вашей квартиры» и «конченые наркоманы»:
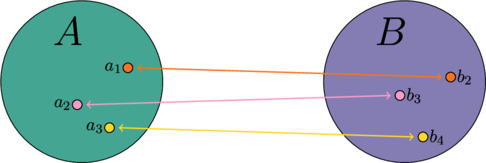
Как было сказано, чем больше элементов, то есть знаний о том, как их связывать с чем-то ещё, тем больше и печалей, т.е. необходимости всё это держать в уме. Куда проще всё могло оказаться, будь у нас какое-то правило, которое достаточно будет выучить, после чего мы безошибочно сможем, отталкиваясь от одного элемента, как по ниточке, прийти к другому. И ведь такое правило задать действительно можно, да ещё и назвать его как-то вроде ![]() :
:
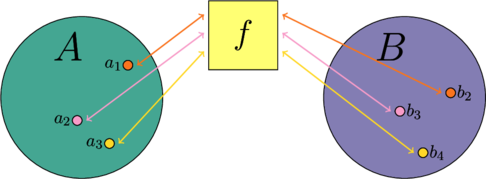
Смотрите, смысл иллюстрации состоит в том, что у нас есть изначальное множество ![]() , затем у нас есть некое правило, инструкция по трансформации, если хотите, просто фильтр или чёрный ящик
, затем у нас есть некое правило, инструкция по трансформации, если хотите, просто фильтр или чёрный ящик ![]() , проходя через который наш элемент
, проходя через который наш элемент ![]() становится некоторым
становится некоторым ![]() . В указанном выше случае перевода
. В указанном выше случае перевода ![]() в
в ![]() и т.п. это правило можно заметить без лишнего труда, ведь мы просто переводим элемент одного множества в элемент другого, но который идёт дальше по порядку.
и т.п. это правило можно заметить без лишнего труда, ведь мы просто переводим элемент одного множества в элемент другого, но который идёт дальше по порядку.
Запишем правило в общем виде, получив ![]() . Готово, теперь в нашем распоряжении оказалась чёткая, ровная инструкция для получения одного элемента из другого. В принципе, это всё, что надо знать о функциональной зависимости. Добавить к этому следует лишь некоторую терминологию.
. Готово, теперь в нашем распоряжении оказалась чёткая, ровная инструкция для получения одного элемента из другого. В принципе, это всё, что надо знать о функциональной зависимости. Добавить к этому следует лишь некоторую терминологию.
К примеру, само правило ![]() , по которому мы переводим одно в другое, называется «функцией». Хотя нет, в реальности «функцией» называют что-то типа
, по которому мы переводим одно в другое, называется «функцией». Хотя нет, в реальности «функцией» называют что-то типа ![]() , но это не функция, а значение функции в точке
, но это не функция, а значение функции в точке ![]() (в многочисленных учебниках этого различения также не делают).
(в многочисленных учебниках этого различения также не делают).

Я вот всё-таки не могу терпеть и скажу, что ![]() это реально очень, очень плохой способ записывать функцию. Популярен он стал благодаря французскому математику Клоду Клеро, который его в употребление и ввёл. Куда логичнее было бы писать
это реально очень, очень плохой способ записывать функцию. Популярен он стал благодаря французскому математику Клоду Клеро, который его в употребление и ввёл. Куда логичнее было бы писать ![]() , чтобы сразу видеть, как переменная через что-то проходит. Но нет, все пишут именно
, чтобы сразу видеть, как переменная через что-то проходит. Но нет, все пишут именно ![]() , хотя в итоге это приходится читать справа налево, чтобы не возникало лишних вопросов.
, хотя в итоге это приходится читать справа налево, чтобы не возникало лишних вопросов.
Множество ![]() называется «областью определения функции» (domain), то есть, всем тем исходным материалом, колдуя над которым мы и получаем конкретные значения.
называется «областью определения функции» (domain), то есть, всем тем исходным материалом, колдуя над которым мы и получаем конкретные значения.
Множество ![]() называется «областью значений функции» (codomain), то есть, речь идёт о всём том, что мы получаем, пропустив элементы
называется «областью значений функции» (codomain), то есть, речь идёт о всём том, что мы получаем, пропустив элементы ![]() через специально определённый фильтр
через специально определённый фильтр ![]() .
.
К этому процессу, кстати, есть несколько требований. Пожалуй, самое важное из них — каждому ![]() может соответствовать только одно
может соответствовать только одно ![]() , иначе функциональная связь ломается. Когда преподаватель говорит, что надо «найти функцию
, иначе функциональная связь ломается. Когда преподаватель говорит, что надо «найти функцию ![]() «, то он сам не ведает, что творит. Ведь в чём смысл функциональной взаимосвязи? Он в том, что мы можем чётко установить соответствие между одним элементом из
«, то он сам не ведает, что творит. Ведь в чём смысл функциональной взаимосвязи? Он в том, что мы можем чётко установить соответствие между одним элементом из ![]() и другим элементом из
и другим элементом из ![]() .
.
А что получается с корнем? Допустим, мы ищем ![]() . Получаем два ответа, равные
. Получаем два ответа, равные ![]() и
и ![]() … и как теперь понять, что было нашим изначальным
… и как теперь понять, что было нашим изначальным ![]() ? Обычная двойка или её отрицательный вариант? Именно поэтому категорически нельзя, чтобы
? Обычная двойка или её отрицательный вариант? Именно поэтому категорически нельзя, чтобы ![]() мог превратиться во что-то, кроме одного единственного элемента
мог превратиться во что-то, кроме одного единственного элемента ![]() . Обратное, кстати, не верно — несколько
. Обратное, кстати, не верно — несколько ![]() могут превращаться в один и тот же
могут превращаться в один и тот же ![]() и это никак не помешает его при необходимости восстановить, как в случае
и это никак не помешает его при необходимости восстановить, как в случае ![]() , который совершенно точно является примером нормальной функции.
, который совершенно точно является примером нормальной функции.

Вообще, далеко не для любой функции мы обязаны иметь возможность найти изначальные элементы. К примеру, функция ![]() переводит все элементы в ноль, поэтому сказать, что там в начале было, у нас не получится. Тем не менее, главному условию функции такой пример полностью соответствует. А вот корень не соответствует!!
переводит все элементы в ноль, поэтому сказать, что там в начале было, у нас не получится. Тем не менее, главному условию функции такой пример полностью соответствует. А вот корень не соответствует!!
Все ![]() , на практике обозначаемые как
, на практике обозначаемые как ![]() , называются «аргументами функции», или «независимыми переменными», ведь при выборе их мы не зависим ни от чего, кроме личных предпочтений.
, называются «аргументами функции», или «независимыми переменными», ведь при выборе их мы не зависим ни от чего, кроме личных предпочтений.
Наконец, ![]() называют «значением функции», хотя в реальной жизни, как уже было отмечено, имеет место распространённая ошибка, когда про
называют «значением функции», хотя в реальной жизни, как уже было отмечено, имеет место распространённая ошибка, когда про ![]() говорят, что это просто «функция от
говорят, что это просто «функция от ![]() «, что, конечно, не так, ведь функция — это само правило
«, что, конечно, не так, ведь функция — это само правило ![]() для сопоставления элементов, а не отдельно взятое значение для частного случая.
для сопоставления элементов, а не отдельно взятое значение для частного случая.
До сих пор мы говорили про функции как отображения между несколькими множествами, однако это далеко не вся картина. Вполне возможно представить себе правило и для отображения множества на себя самого. То есть, одному элементу ставится в соответствие другой, из того же множества (или из точно такого же), и так далее. Подавляющее большинство изучаемых функций именно такие — там рассматриваются отображения типа ![]() , которые из одних чисел делают другие, а уж нам остаётся весь этот процесс рассмотреть детальнее. Но это будет уже совсем другая история, которая начнётся с раскрытия смысла множества
, которые из одних чисел делают другие, а уж нам остаётся весь этот процесс рассмотреть детальнее. Но это будет уже совсем другая история, которая начнётся с раскрытия смысла множества ![]() …
…
Comments ( 6 )