Ну как, чувствуется эффект от плавного вхождения в область практической математики? Теперь уже получится различные действия выполнять, примеры решать, да и у бочки с квасом летом можно спокойно занимать очередь — со сдачей не обманут. Прямо и хочется спросить: а к чему были все эти цветастые кубики и прочие детские заискивания? Формальная запись ведь обладает несравненным преимуществом, ей всё в любом случае и закончится, разве не так?
Для многих задач это действительно так, однако мощь визуализации не стоит недооценивать. К тому же строгие формулы и яркие рисунки вполне можно между собой подружить во имя общего блага. Рассмотрим это на примере, познакомившись с ещё одним символом, греческой заглавной буквой сигма:
![]()
Зачем она нужна? Как и многие математические символы, её использование заметно упрощает жизнь, экономит время, помогает личностному росту и карьерным амбициям. Допустим, что нам пришлось ответить на следующий вопрос: какова сумма следующих друг за другом чисел натурального ряда, начиная с первого? Причём нам не просто надо подсчитать значение ![]() , а дать универсальный ответ или хотя бы алгоритм. Хотите сказать, что мы ничего ещё не успели пройти, чтобы от вас такое требовать? Эх, вечно вы себя недооцениваете…
, а дать универсальный ответ или хотя бы алгоритм. Хотите сказать, что мы ничего ещё не успели пройти, чтобы от вас такое требовать? Эх, вечно вы себя недооцениваете…
Имея под рукой компьютер или простой калькулятор, разобраться с этим делом легко, если только самих чисел не так много. А что делать в случае ![]() чисел, а если столкнёмся с целой тысячью? Ведь их не так просто не только сложить между собой, но и даже сама запись займёт приличное время. Нужен какой-то способ сократить страдания. Именно для этого нам и нужна сигма, означающая ни что иное, как действие супер-суммирования (ну или просто суммирования, если аналогии из комиксов вам не нравятся). Собственно, это всё то же суммирование, только проделываемое со множеством элементов.
чисел, а если столкнёмся с целой тысячью? Ведь их не так просто не только сложить между собой, но и даже сама запись займёт приличное время. Нужен какой-то способ сократить страдания. Именно для этого нам и нужна сигма, означающая ни что иное, как действие супер-суммирования (ну или просто суммирования, если аналогии из комиксов вам не нравятся). Собственно, это всё то же суммирование, только проделываемое со множеством элементов.
Сигма требует указать верхний и нижний предел проводимой операции. Скажем, мы хотим сложить первые ![]() натуральных чисел, как быть? Да просто, мы указываем нижний предел, с которого начинаем (то есть единицу) и верхний, на котором остановится, то есть пятёрку.
натуральных чисел, как быть? Да просто, мы указываем нижний предел, с которого начинаем (то есть единицу) и верхний, на котором остановится, то есть пятёрку.
![Rendered by QuickLaTeX.com \[\sum_{a=1}^{5}a_i=a_1+a_2+a_3+a_4+a_5\]](http://popmath.ru/wp-content/ql-cache/quicklatex.com-5b86d7cde7bcc0852abd9f33ec2d4c45_l3.png)
Расшифровывается это так: сумма всех элементов типа ![]() , принимающих значения, начиная с
, принимающих значения, начиная с ![]() и заканчивая
и заканчивая ![]() . В нашем случае подразумевается, что
. В нашем случае подразумевается, что ![]() , т.е.
, т.е. ![]() и тому подобное. Но перед нами то стоит вопрос не про конкретную пятёрку, а про сумму последовательных натуральных чисел вообще. Значит, требуется вывести следующую формулу.
и тому подобное. Но перед нами то стоит вопрос не про конкретную пятёрку, а про сумму последовательных натуральных чисел вообще. Значит, требуется вывести следующую формулу.
![Rendered by QuickLaTeX.com \[\sum_{a=1}^{n}a_i=?\]](http://popmath.ru/wp-content/ql-cache/quicklatex.com-2f165bfd62510b0be94188fa243b3eef_l3.png)
Буква ![]() означает, что вместо неё мы можем поставить какое угодно число, и каждый раз должны получить верный ответ. Сложновато? Тогда призовём на помощь кубики, которым мы так легкомысленно чуть не указали на дверь. Как мы помним, сложение это движение вправо по числовой оси. Давайте разместим хотя бы
означает, что вместо неё мы можем поставить какое угодно число, и каждый раз должны получить верный ответ. Сложновато? Тогда призовём на помощь кубики, которым мы так легкомысленно чуть не указали на дверь. Как мы помним, сложение это движение вправо по числовой оси. Давайте разместим хотя бы ![]() первых числа таким образом и посмотрим, к чему это приведёт:
первых числа таким образом и посмотрим, к чему это приведёт:

Глаз всё это безусловно радует, однако отдаёт излишней громоздкостью. В точке ![]() мы оказались, но и слагаемых ведь у нас было только
мы оказались, но и слагаемых ведь у нас было только ![]() , сколько же понадобится бумаги или часов стучания по клавишам, чтобы разобраться с более сложными примерами? Да и конкретного алгоритма мы так и не выработали.
, сколько же понадобится бумаги или часов стучания по клавишам, чтобы разобраться с более сложными примерами? Да и конкретного алгоритма мы так и не выработали.
Прибегнем к другому способу компановки, разместив все числа-блоки вертикально, в аккуратную лесенку, добавив вторую ось. Ну и ради наглядности (всё равно ведь рисованием занялись) увеличим количество слагаемых до ![]() :
:
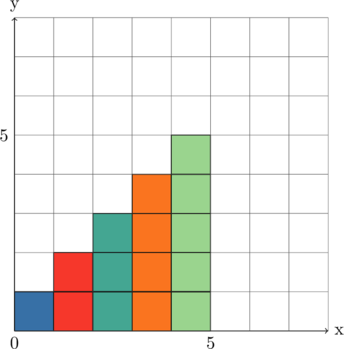
Получилось заметно компактнее, страницу больше не разрывает. Однако по-прежнему не понятно, как всё это посчитать. Впрочем, можно же представить, что ситуация внезапно решила сложиться самым благоприятным для нас образом и недостающие пропуски сами собой заполнились нежнейшей розовой материей, создав следующую картину?
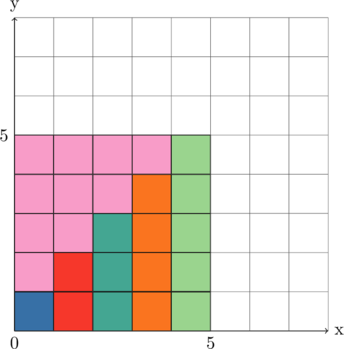
С цельной плиткой дела иметь всяко удобнее. Да и потом, вспомнив, как мы определяли умножение, найти количество кубиков (а значит, и сумму всех чисел) в рамках такой плитки намного проще, достаточно умножить ещё ширину на высоту, получив в данном случае ![]() . Проблема лишь в том, что из этого числа нам придётся вычесть всю ту розовую сумму, которую мы искусственно добавили, то есть найти сумму
. Проблема лишь в том, что из этого числа нам придётся вычесть всю ту розовую сумму, которую мы искусственно добавили, то есть найти сумму ![]() , которая у нас уже дала выше десятку. Если же решать не ручками, а по-уму, то эта задача ожидаемо сведётся к поиску суммы
, которая у нас уже дала выше десятку. Если же решать не ручками, а по-уму, то эта задача ожидаемо сведётся к поиску суммы ![]() , потом к поиску
, потом к поиску ![]() и т.п. И да, ещё раз — что делать, если слагаемых несколько тысяч?
и т.п. И да, ещё раз — что делать, если слагаемых несколько тысяч?
Избежать всего этого жестокого цикла можно было бы, будь у нас возможность как-то легко вычленить всю ту лишнюю массу, которую мы добавили, не суммируя её отдельный составляющие… и эта возможность у нас есть. Давайте отодвинем всю конструкцию на одну единицу вправо и добавим новую, тоже розовую (но несколько более тёмную) колонку, в которой будет ровно пять элементов:
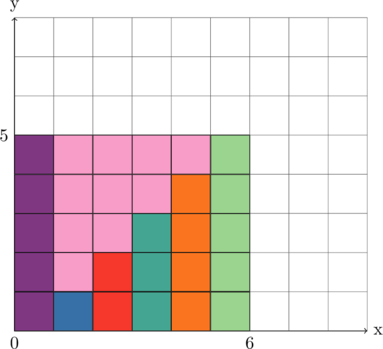
Теперь-то мы в итоге добавили точно столько кубиков, сколько содержалось в изначальном задании. Посчитать их общее количество по-прежнему просто, нужно всего лишь умножить ![]() на
на ![]() (ведь мы добавили одну колонку, увеличив ширину), получаем
(ведь мы добавили одну колонку, увеличив ширину), получаем ![]() , которое теперь делим пополам, чтобы узнать изначально данную нам сумму.
, которое теперь делим пополам, чтобы узнать изначально данную нам сумму.
![Rendered by QuickLaTeX.com \[\sum_{a=1}^{5}a_i=15\]](http://popmath.ru/wp-content/ql-cache/quicklatex.com-a396ceef2643edc7f7e57122965de239_l3.png)
Неплохо. Но всё же, как нам получить общую формулу? Минуточку…. матерь божья, так мы это уже сделали! Независимо от заданного количества чисел ![]() , мы всегда можем удвоить их количество, найти сумму кубиков в получившейся фигуре (умножив
, мы всегда можем удвоить их количество, найти сумму кубиков в получившейся фигуре (умножив ![]() на
на ![]() , т.к. ширина фигуры увеличилась на
, т.к. ширина фигуры увеличилась на ![]() ) и разделить её на два. Запишем свои достижения формально.
) и разделить её на два. Запишем свои достижения формально.
![Rendered by QuickLaTeX.com \[\sum_{a=1}^{n}a_i=n\cdot x:2\]](http://popmath.ru/wp-content/ql-cache/quicklatex.com-a9f91ccbcf1e13c70fd87ade6e1ee513_l3.png)
Перед нами крайне изящная формула, известная как формула Гаусса. Согласно легенде, чтобы справиться со слишком активным Карлом Гауссом (это такой великий математик, если что), учитель поручил ему сосчитать сумму натуральных чисел от ![]() до
до ![]() , полагая, что выиграл этим какое-то время. Однако Гаусс, даже будучи ребёнком, оказался не так прост и дал ответ почти моментально. Правда? кубиками он не пользовался.
, полагая, что выиграл этим какое-то время. Однако Гаусс, даже будучи ребёнком, оказался не так прост и дал ответ почти моментально. Правда? кубиками он не пользовался.
главная догадка у него состояла в ином. Он заметил, что ряд натуральных чисел очень удобно разбивается на пары. В случае, если само количество чисел чётное (то есть, может быть разделено на ![]() ), то таких пар будет ровно в два раза меньше, чем индивидуальных чисел. Причём существует некая центральная точка, двигаясь от которой в разные стороны, мы будем наблюдать либо возрастание, либо уменьшение этих чисел равным темпом.
), то таких пар будет ровно в два раза меньше, чем индивидуальных чисел. Причём существует некая центральная точка, двигаясь от которой в разные стороны, мы будем наблюдать либо возрастание, либо уменьшение этих чисел равным темпом.
Поясним рисунком (клянёмся, больше никаких кубиков). Раз уж речь зашла о чётных числах, то возьмём восьмёрку. Ну и ноль рисовать не будем, учитывая, что на сумму он всё равно никак влиять не будет.
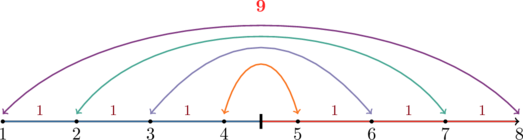
Итак, мы выбрали точку, делящую наш фрагмент числовой прямой ровно пополам. Из неё мы начали движение в двух разных направлениях, одновременно формируя пары ![]() и
и ![]() ,
, ![]() и
и ![]() и так далее. Для этих пар можно заметить вот что — чем больше становится одно число, тем меньше другое, причём если одно становится на единицу больше, то другое на эту же единицу уменьшается. Что это нам говорит? А то, что сумма остаётся неизменной! Значит, если у нас получилось
и так далее. Для этих пар можно заметить вот что — чем больше становится одно число, тем меньше другое, причём если одно становится на единицу больше, то другое на эту же единицу уменьшается. Что это нам говорит? А то, что сумма остаётся неизменной! Значит, если у нас получилось ![]() пары, дающих каждая в сумме по
пары, дающих каждая в сумме по ![]() , то там достаточно просто умножить эту девятку на количество пар, то есть
, то там достаточно просто умножить эту девятку на количество пар, то есть ![]() , что полностью повторяет своими результатами формулу, выведенную нами слегка выше.
, что полностью повторяет своими результатами формулу, выведенную нами слегка выше.
Ситуация с чётностью хлопот не доставила. Ну а если количество чисел не чётно? чтобы далеко не ходить за примером, давайте проверим, что делать в случае ![]() .
.
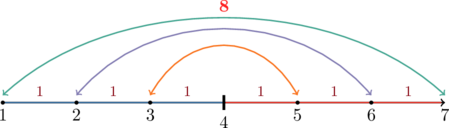
Тут дело похожее, но не совсем. Во-первых, центром нашего отрезка становится точка, соответствующая числу ![]() . Во-вторых, формируемых пар у нас получается
. Во-вторых, формируемых пар у нас получается ![]() , вот только для четвёрки места нет, ей остаётся лишь одиночество, тёплый свитер и затяжная депрессия. Впрочем,
, вот только для четвёрки места нет, ей остаётся лишь одиночество, тёплый свитер и затяжная депрессия. Впрочем, ![]() всё же обладает интересной особенностью — она является ровно половиной от суммы получающихся пар. Выходит, что каждая пара распадается на две таких четвёрки, плюс ещё одна, которая стоит в одиночестве, итого, мы умножаем все эти четвёрки (полученные делением суммы пар пополам) на их общее количество, т.е. на
всё же обладает интересной особенностью — она является ровно половиной от суммы получающихся пар. Выходит, что каждая пара распадается на две таких четвёрки, плюс ещё одна, которая стоит в одиночестве, итого, мы умножаем все эти четвёрки (полученные делением суммы пар пополам) на их общее количество, т.е. на ![]() , получая
, получая ![]() .
.
То, что мы пришли к одинаковому результату, используя разные исходные идеи, не должно удивлять. Точнее, должно, но в хорошем смысле, так как это само по себе замечательное явление. Оно означает, что не обязательно долбиться лбом в дверь, если можно пролезть через окно. Ну а вообще, для серьёзных математиков, доказывающих мудрёные вещи, видеть связь между самыми различными областями науки, исследовать явление типа со всех возможных сторон — крайне важно.

Если оно с одной стороны не поддаётся, то ты его с другой попробуй, надо слабое место найти и в него бить. Я вот в прошлом месяце на соревнованиях пытался вообще ударами в ухо паренька размотать, а он ни в какую. Ну я проходочку в ноги сделал, а там уже, как Хабиб, локтями на земле и забил. С задачей так же надо, совсем как в ММА.
Comment ( 1 )