Путь натурала

До сих пор пройденный материал был достаточно абстрактным. Мы говорили об операциях, отношениях, прочих взаимосвязях и особенностях, но в каком-то очень неконкретном, мутном виде. Как всё это может помочь нам в реальном мире, где необходимо считать яблоки, взвешивать колбасу и оплачивать услуги ЖКХ? Теория множеств нам тут уже не помощник, требуются куда более детальные знания. Раз так, то давайте к ним без замедления переходить.

Но для начала вернёмся к примеру с холодильником из начала прошлой статьи. Давайте немного наполним  его содержанием, используя, конечно же, всё те же чудные цветастые кружочки.

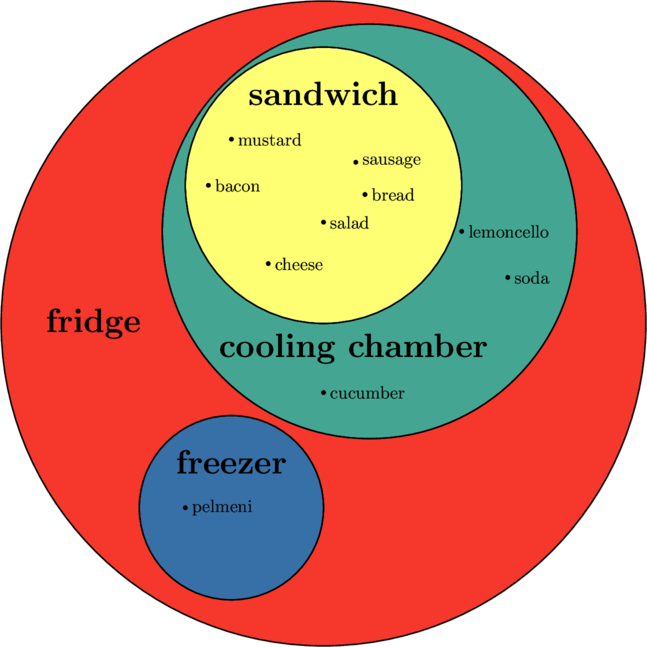
Что мы из этого видим? Например, мы предпочитаем сэндвичи, состоящие из колбасы, сыра, бекона и листьев салата с горчицей, это всё помимо хлебушка. Кроме того, где-то на соседних полках у нас разместились огурчики, газировка и даже относительно полная бутылка Лемончелло. Ну а в морозильной камере, конечно, пельмешки, куда без них, особенно под конец месяца? Все названия на английском не из-за желания походить на хипстеров, просто с поддержкой кириллицы у QuickLaTeX большие проблемы.

Гастрономический экскурс полезен ещё и следующим. Видно, что, например, колбаса, являющаяся элементом сэнвдича и обозначенная точкой, также является элементом всей холодильной камеры, да и холодильника вообще. Схожая принадлежность есть и огурчиков. И даже морозилка, хотя и не имеет общих элементов с холодильной камерой, всё равно выступает подмножеством холодильника.

Именно эту идею расширяющихся подмножеств мы спешим использовать в первой из наших статей, которую можно назвать «чисто конкретной» (оценили шутку?).

 

Натуральные числа и смысл сложения

Для большинства бытовых операций люди, как вы, наверное, знаете, используют всевозможные числа. Что такое число? А никто и не знает. Серьёзно, это ещё одно из неформализуемых математических понятий, которые нам предстоит активно использовать. Можно считать, что это некая обобщённая идея «количества», только поддающаяся дифференциации, типа, количество, которое можно отличать от другого количества. Для записи чисел используются цифры, в частности, арабские, основывающиеся на десятичной системе счисления.

Пожалуй, самым частым примером неправильного использования терминов может служить извечная путаница между «числом» и «цифрой». В тех же новостных выпусках регулярно говорят про «огромную цифру», политики любят пафосно рассуждать о «недопустимых цифрах» и тому подобное. Увы, цифр в нашей системе счёта всего , вот они, полюбуйтесь: . Благодаря им можно записывать любые числа, например, , только «одна тысяча пятьсот тридцать четыре» это число, означающее некое количество, которое лишь записано при помощи цифр. Решительно протестуйте против любых попыток ввести вас в заблуждение путём подмены понятий!

 

Самым базовым примером чисел являются числа натуральные. Отчего это они натуральные? Видимо предполагается, что они неизбежно возникают при попытке что-либо в реальности пересчитать, хотя бы по пальцам. Как строятся натуральные числа? Не утомляясь подробностями аксиоматики, можно представить их как постепенное возрастание некоего единого и неделимого. Это единое обозначается цифрой , называется единицей.

После того, как мы получили свою первую единицу, мы можем получить много, бесконечно много точно таких же единиц. Что нам со всем этим добром делать? Его можно складывать. Сложение есть некая операция (мы же не зря про операции столько говорили), обозначаемая символом . Например, , и тому подобное. Элементы, которые складываются, называются «слагаемыми», а результат сложения — «суммой».

 

Натуральное число. Число называется натуральным, если оно может быть получено только путём «совмещения» любого количества равных себе чисел, называемых «единицами».

 

Постепенно прибавляя единицу снова и снова, мы получаем ряд натуральных чисел, , и так, заметьте, до бесконечности. В этом принципиальное отличие натуральных чисел от «продуктовых» множеств, которые нам приходилось рассматривать ранее. Множество натуральных чисел, обозначаемое буквой , принципиально бесконечно. Оно вроде понятно, ведь ничто не мешает нам прибавлять единицу снова, снова и снова. Вы заметили, что — вовсе не обычная ? Это различие нужно не для того чтобы сбить вас с толку, просто, как уже говорилось, букв в алфавите не так много, потому для обозначения каких-то конкретных множеств и используются отдельные шрифты.

И всё же, что такое сложение? Описать это адекватным образом едва ли возможно. Приходится прибегать к синонимам вроде «слияния», «совмещения» и тому подобного. Эмпирические исследования показывают, что некие понятия о сложении и основах счёта есть не только у людей, пусть и очень юных, но и у приматов, птиц и даже слонов. Поэтому будем полагаться на интуитивную доступность понятия.

 

Сложение (суммирование). Сложением называется бинарная операция, обозначаемая знаком (плюс). Например, , тогда — слагаемые, — сумма (результат сложения).

 

Впрочем, если нечто нельзя объяснить, это не значит, что его нельзя проиллюстрировать.

Вообразим себе прямую линию, направленную в одну сторону. Мы делим эту линию на равные части достаточно простым образом: замеряем любое расстояние, говорим, что оно равно единице, после чего используем это расстояние для последующего расчленения.

 

 

Строго говоря, то, что мы нарисовали, это не линия. В математике когда говорят про прямую линию (line), то подразумевают, что она бесконечно продолжается в обе стороны. В нашем же случае есть совершенно явное начало в точке , хотя вправо мы предполагаем бесконечное продолжение. Это значит, что мы имеем дело с лучом (ray), который бесконечен лишь по одному направлению. Если бы мы решили чётко зафиксировать не только начало, но и конец, то в итоге получили бы отрезок (line segment). 

 

 

Дополнительно обратим внимание, что каждая следующая точка отстоит от предыдущей ровно на единицу, в этом весь принцип натуральных чисел — следующие друг за другом числа могут отличаться только на единицу, никак иначе, ведь любое натуральное число может состоять только из какого-то количества единиц.

Опять небольшой тест на память — припоминаете абзацы про кардинальные числа множеств? Это такие числа, которые показывают количество элементов в множестве, если что. Так вот, возьмём пустое множество, начнём добавлять в него поочерёдно всё новые и новые элементы, тогда кардинальные числа этих последовательных множеств как раз и составят ряд натуральных чисел (или, как ещё говорят, «натуральный ряд»).

Сложно поверить, но среди математиков есть совершенно противоположные мнения на тему того, считать ли сам ноль натуральным числом или нет. С одной стороны, у него масса особенностей и отличий от остальных натуральных чисел. С другой стороны, ноль вполне может использоваться при «естественном» счёте, может же у вас в холодильнике не быть яблок? Какого мнения стоит придерживаться, будем уточнять по ситуации.

Вернёмся к картинке. Учитывая всё описанное, сложение можно описать как движение по нашей… как бы её назвать… числовой оси. Находясь в точке , мы, сделав три шага по (или, что то же самое, один шаг длиной в ), переходим к точке . Из мы уже перемещаемся в за шагов, ну и тому подобное. Цветовое выделение участков добавляем исключительно ради наглядности:

 

Как понимать умножение?

Разобравшись с пошаговым сложением, давайте познакомимся с его модифицированной версией — умножением. Для обозначения умножения используется несколько знаков, нечто похожее на крест и точка , располагающаяся не снизу, а посередине строки. Учитывая это, и означает одно и то же, хотя на практике точка используется намного чаще. Тут тоже не обошлось без хитрости. Если мы имеем дело не с цифрами, а другими символами, теми же буквами, то точку предпочитают не ставить, вместо пишут просто . С числами такой трюк не пройдёт. Элементы, которые умножаются, называются «множителями», а результат умножения — «произведение».

 

Умножение. Умножением называется бинарная операция, обозначающаяся символами в случае с числами (например, ), либо не обозначающаяся никак в случае с символами (например, ). Если , то — множители, а — произведение (результат умножения).

 

Понятненько? Если да, то самое время спросить в чём состоит идея умножения, не таит ли она в себе столько же подводных камней, сколько правила её формальной записи? Устав от буковок, вновь прибегнем к рисункам.

Перед нами теперь уже знакомая числовая ось, вот только единичные деления теперь состоят из кубиков, которых всего шесть (можете пересчитать). Почему они окрашены в разные цвета? А потому, что мы решили разделить наши кубиков на равных блока, каждый блок содержит ровно по кубика. Получается, что нашу шестёрку мы можем, используя сложение, записать как . Вроде удобно, но что если мы захотим записать таким образом число , либо , либо и так далее? Столько двоек и знаков сложения выводить было бы скучно. Поэтому мы прибегаем к сокращению — вместо того, чтобы писать , мы записываем .

Понимать это следует напрямую: шесть состоит из трёх блоков по две единицы (ну или по два «кубика»). Можно прочесть запись и задом наперёд, сказав, что , ну или , то есть, что шесть состоит из двух блоков по три, в таком случае иллюстрацию следует слегка изменить:

Как видим, в итоге мы всё равно имеем те же самые шесть кубиков, только полученные несколько иной комбинацией. Конечно, можно записать всё и как , и даже , но изобразить это вы уже можете самостоятельно. Главное, что надо понимать, это что умножение есть операция, производная от сложения, её сокращённый, «ленивый» вариант. Если в сложении элементы, над которыми производится операция, называются слагаемыми, то в случае умножения эти самые элементы зовутся множителями. Думаете, мы эти названия повторяем от нечего делать?

Важное свойство, объединяющее две операции, которое вы конечно же помните из первых статей, называется коммутативность. А именно, совершенно не важно, в каком порядке стоят элементы, будет означать «два шага вправо от пяти», а будет значить «пять шагов вправо от двух», в итоге мы всё равно попадём в точку , ну или получим семь кубиков. То же верно и для умножения, ведь мы уже видели, что и никак не влияют на получившееся количество элементов. Именно поэтому у нас при выполнении операций есть два слагаемых и два множителя, названных совершенно одинаково!

Для чего вообще задумываться о какой-то коммутативности? А для того, что это сильно расширяет пространство для творчества. Допустим, вам задали пример типа , считать его откровенно не хочется, а открыть калькулятор на мобильном телефоне не даёт бдительный преподаватель. Зная, что сложение коммутативно, вы вольны выполнять операции в каком угодно порядке, например, поменять местами слагаемые так, чтобы получилось , где соседние слагаемые дают в сумме по десятке, а финальным ответом будет . Видите, только что мы сэкономили кучу времени, которое теперь можно потратить на онлайн-игры.

Подобный трюк можно провернуть и с умножением, тогда всякие можно решать вообще с конца, умножив на , затем умножив полученную десятку на , а уж потом домножить на оставшуюся семёрку, получив столь милое сердцу . Вы удивитесь, когда поймёте, какое невероятное количество школьных и вузовских заданий требуют от вас таких перестановок.

 

Нет, нет и нет!! Боже, у меня сейчас сердце из груди  выпрыгнет! В примере , к которому мы пришли коммутативными перестановками, рядом стоящие слагаемые и правда дают в сумме по десятке. Но то, что мы их можем складывать в любом порядке, зависит не от коммутативности, а от свойства ассоциативности! То есть, , а уж в каком порядке выполнять операции — наше дело… Как это «какая разница»? Вы вообще представляете, какую ошибку чуть не сделали??

 

 

При всём этом мы не успели сказать о совершенно особенной роли  числа ноль. Если сложение (когда вы что-то складываете, то получаете «сумму чисел») любого числа с нулём никак его не меняет, , т.к. это дословно значит «не делать никаких шагов от «, то с умножением наоборот. Если ноль является одним из множителей (то, что дают множители при перемножении, это «произведение»), то весь итог оказывается равен нулю. Подумайте об этом, что означает ? Надо взять шесть блоков, состоящих из… ничего. Помнить это просто необходимо, ведь при взгляде на мы сразу выхватываем зрением ноль и заключаем, что всё произведение равно нулю.

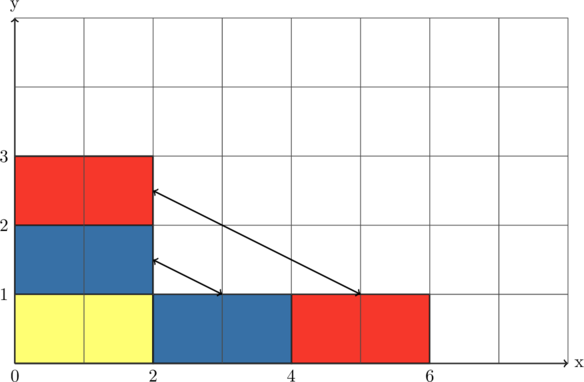
Раз уж мы завели речь про память, то давайте проверим, что у вас с её краткосрочным вариантом. Мы тут совсем недавно говорили о сложении как о путешествии по числовой оси, заодно изобразили симпатичную картиночку.

 

Вычитание и деление

Заметно ли в ней что-то, кроме утончённого художественного вкуса автора? Оказывается, что заметно — стрелочки стоят на обоих концах кривых, призванных символизировать переход по числовой оси. Это означает, что путешествие можно совершать в обе стороны. Например, вернуться из в , совершив шагов влево. Исключительно благодаря двойным стрелочкам мы приходим к новой операции, обратной (раз уж мы движемся в обратную сторону) сложению. Называется она вычитание и обозначается знаком , который называется минус.

Движение влево на нашей оси, из в , например, записывается как . При этом называется уменьшаемым, зовётся вычитаемым, ну а для уготовано разность. Не видите ничего подозрительного?

 

Вычитание. Вычитанием называется бинарная операция, обозначаемая знаком (минус). Допустим, , тогда — уменьшаемое, — вычитаемое, а — разность (результат вычитания).

 

В случае со сложением и умножением оба операнда (т.е. элемента, над которыми проводилась операция) назывались «слагаемыми» либо «множителями», т.е. одинаково. А вот с вычитанием два элемента внезапно зовутся по-разному. С чего бы это? А с того, что вычитание не является коммутативной операцией!

Действительно, давайте запишем , отмерив три шага влево, мы окажемся в точке (или же в активе будет два кубика), . Изменим условия игры, записав , тогда мы получим… а мы ничего не получим. Условившись, что наша числовая ось начинается с точки «ноль», мы заранее обрекли себя на невозможность путешествовать влево столько, сколько захочется. В случае мы приходим к нулю за три шага, но у нас остаётся необходимость совершить ещё два, чего мы сделать принципиально не можем. Остаётся признать, что в случае со множеством натуральных чисел, то есть с , результата операции просто не существует.

Секундочку… А что же с умножением? Какое обратное действие можно найти составлению числа из фиксированных блоков? Ну, можно попробовать это число на эти самые блоки разложить. Для этого нам понадобится операция деления. Запишем , здесь мы задаёмся вопросом, сколько элементов будут содержать два одинаковых по размеру блока, на которые мы расчленим шестёрку. Само число это делимое, — делитель, а — частное. По аналогии с тем, что мы делали при умножении, . Уф, да мы просто боги деконструкции!

 

Деление. Делением называется бинарная операция, обозначаемая символами . Допустим, , тогда — делимое, — делитель, — частное (результат деления).

 

Посчитаем ещё что-то, к примеру, , и получим… конечно же, ничего. Мы не можем подобрать такого числа среди натуральных, чтобы оно подошло на роль результата данной операции. И да, учитывая, что у операндов опять разные названия, то деление не является коммутативным, если , то нам вообще ничего не даёт. Ноль на помощь подоспеть тоже не в состоянии. Напротив, делить что-то на ноль нельзя в принципе, поэтому запись типа не имеет смысла. В школе говорят, что это некая «запретная операция», создавая вокруг неё ореол мрачной тайны. На самом деле она просто не может быть корректно определена, ведь разделение чего-то на несуществующее количество частей у людей непротиворечиво описать так и не получилось.

 

Замкнутость множеств и роль перестановок

Удивительные особенности, обнаруженные в ходе казалось бы простого рассуждения, знакомят нас с интересным концептом замкнутости. Множество называется замкнутым относительно какой-то операции, если мы можем проводить её сколько угодно, с каким угодно количеством элементов, и в итоге каждый раз будем получать элемент, содержащийся в множестве, т.е. не покинем его границы.

 

 

 

Множество замкнуто — значит, можно всё делать, сколько хочется, пока не устанешь. Когда не замкнуто, то надо уважать правила, по беспределу угарать всё время не получится, лишь самому хуже станет.

 

 

В случае с наше множество замкнуто относительно сложения и умножения, ведь путешествовать вправо мы можем сколько угодно. А вот для вычитания и деления мы вынуждены установить строгие правила поведения, иначе рискуем получить бессмыслицу. Задав такие правила, мы как приличные люди оказываемся обязаны найти способ их нарушить, чем будем прицельно заниматься в следующих статьях.

А пока что напоследок упомянем о ещё одной достаточно важной идее, которая воплощена в уже полюбившихся всем кубиках. Разделение некоего их количества на составляющие блоки это далеко не всё, чем можно заниматься. С практической точки зрения куда полезнее оказывается возможность этими кубиками бессовестно манипулировать.

Само собой, имея перед собой лишь одну числовую ось, устремлённую в бесконечность, особо не поиграешь, разве что положишь кубики или чуть дальше, или чуть ближе. Поэтому мы горизонты свободы расширяем, добавляя ещё одну ось таким образом, чтобы в итоге получить подобие креста. Оставаясь в рамках натуральных чисел, полного креста мы не увидим, но начинать всегда лучше потихоньку, сгодится и усечённый вариант:

Что успело случиться? Как минимум, у нас добавилась вторая ось (про всякие буквы рядом со стрелочками, вроде и , поговорим в другой раз), а вместе с ней и возможность двигаться вверх. Выходит, при желании мы можем не растягивать все шесть кубиков, а сложить их куда компактнее, аккуратной стопочкой. Можно хоть деньги ставить на то, что если вам больше , то нечто подобное вам делать точно приходилось. И дело тут вовсе не в посещении математического кружка или летней подработке мерчендайзером в Пятёрочке. В тетрис же наверняка играли? Основная идея, заложенная в основу этой великой игры, точно такая же — изящная группировка блоков, никак не меняя количество составляющих их элементов, сильно упрощает жизнь.

При выполнении задач  из учебника плотно уложенные фигуры с победной музыкой исчезать не будут, но привычка подвигать элементы туда-сюда, скомпоновав посимпатичнее, окупится многими часами сэкономленного времени.